kategorier: Utvalda artiklar » Intressanta fakta
Antal visningar: 784
Kommentarer till artikeln: 0
Vad är sambandet mellan trådavsnitten och kaninpopulationen?
1202 publicerade den italienska matematikern Leonardo Fibonacci sitt arbete under titeln ”Book of Abacus” (”Book of Calculations”), där han också beskrev nummerserier odödliga med sitt namn. I ett av kapitlen försöker Fibonacci matematiskt visa hur antalet kaniner kommer att öka. Han ansåg följande hypoteser som villkor:
1) de första två månaderna ger ett par kaniner inte avkommor;
2) från och med den tredje månaden ger ett par kaniner ytterligare ett par kaniner.
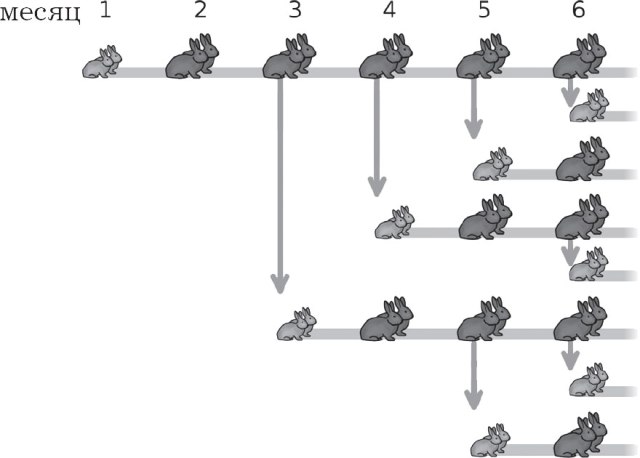
Som ett resultat av att vi konstruerade ett tillväxtmönster för kaninpopulationen, får vi följande antal serier och noterar ökningen av antalet kaniner varje månad:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …
1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…
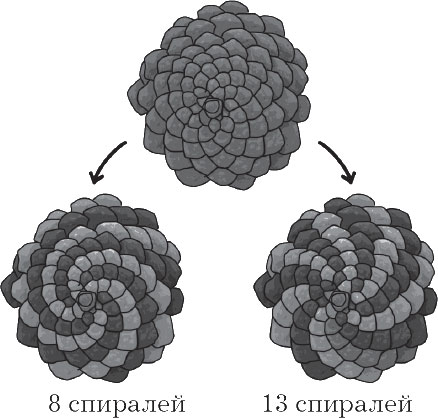
Om du noggrant tittar på ojämnheten kommer du att se att dess yta består av våg som är vridna i en spiral i enlighet med Fibonacci-sekvensen. De är i ananas eller i en solrosblomma, de är synliga för blotta ögat.
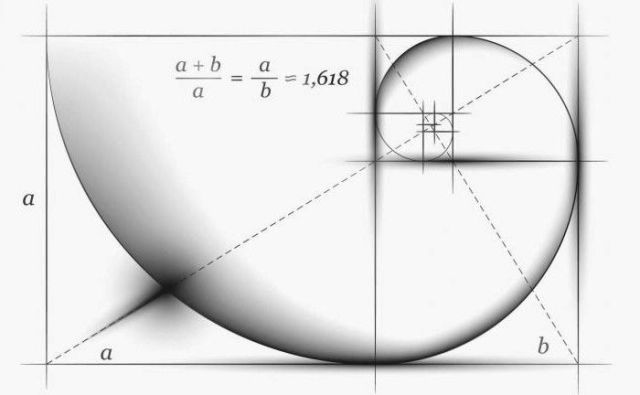
Sedan tiden för antiken av den gyllene förhållandet är antalet = 1.618. De antika grekerna betraktade värdet av en idealisk andel. Det gyllene förhållandet är förhållandet mellan varje efterföljande nummer i Fibonacci-serien till den föregående:
144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...
De gamla grekerna använde det i arkitektur. Fasaden på Parthenon i Aten har mycket lika stora proportioner med en rektangel som bygger på principen om gyllene förhållandet.
Så vad är skönheten i sekvensen av trådtvärsnitt, nominella strömmar av elektriska och avbrottströmmar hos brytare? Bygg en serie med följande värden: 1,5; 2,5; 4; 6; 10; 16; 25; 40; 63...

Nominella strömmar för elektromagnetiska startar:
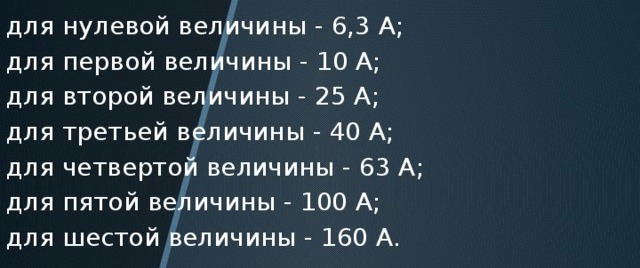
Så om du delar upp 2,5 / 1,5; 4 / 2,5; 6,3 / 4; 10 / 6,3; 16/10; 25/16; 40/25; 63/40då får vi cirka 1,6. Vilket motsvarar den gyllene kvoten regeln. Och återspeglar naturens skönhet och geni även i våra tråkiga tekniksystem.
Vad tror du? Är detta en olycka?
Baserat på boken "En stor roman om matematik. Världshistoria genom matematikens prisma" av Michael Lone. Tack för rekommendationen från Vladimir Kisel.
Alexey Bushnyaga
Se även på elektrohomepro.com
:
