kategorier: Intressanta fakta, Praktisk elektronik
Antal visningar: 231,928
Kommentarer till artikeln: 9
Kondensatorer: ändamål, enhet, princip om drift
 I alla radio- och elektronikapparater, utom transistorer och mikrokretsar, används kondensatorer. I vissa kretsar finns det fler av dem, i andra mindre, men absolut utan kondensatorer finns det praktiskt taget ingen elektronisk krets.
I alla radio- och elektronikapparater, utom transistorer och mikrokretsar, används kondensatorer. I vissa kretsar finns det fler av dem, i andra mindre, men absolut utan kondensatorer finns det praktiskt taget ingen elektronisk krets.
I detta fall kan kondensatorer utföra en mängd olika uppgifter i enheter. Först och främst är det sådana behållare i filtren på likriktare och stabilisatorer. Med hjälp av kondensatorer överförs en signal mellan förstärkningsstegen, låg- och högfrekvensfilter byggs, tidsintervaller i tidsfördröjningar ställs in och svängningsfrekvensen i olika generatorer väljs.
Kondensatorer leder från leiden bankersom i mitten av 1700-talet användes i sina experiment av den holländska forskaren Peter van Mushenbrook. Han bodde i staden Leiden, så det är lätt att gissa varför den här banken kallades.
Egentligen var detta en vanlig glasburk, fodrad inom och utanför med en tennfolie - staniol. Den användes för samma ändamål som modern aluminium, men då var aluminium ännu inte öppen.
Den enda källan till el på dessa dagar var en elektroforemaskin som kunde utveckla en spänning på upp till flera hundra kilovolt. Det var från henne som de anklagade en Leyden-burk. I fysikens läroböcker beskrivs ett fall när Mushenbrook släppte sin burk genom en kedja med tio vakter som håller handen.
Vid den tiden visste ingen att konsekvenserna kunde vara tragiska. Slaget visade sig vara ganska känsligt, men inte dödligt. Det kom inte till detta, eftersom kapaciteten i Leyden-burken var obetydlig, impulsen visade sig vara mycket kortlivad, så att urladdningskraften var liten.
Hur är kondensatorn
Kondensatorns anordning skiljer sig praktiskt taget inte från Leyden-burken: alla samma två plattor, åtskilda med en dielektrik. Således avbildas kondensatorer på moderna elektriska kretsar. Figur 1 visar en schematisk struktur för en platt kondensator och formeln för dess beräkning.
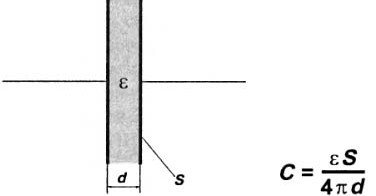
Bild 1. Platt kondensator
Här är S-plattan i kvadratmeter, d är avståndet mellan plattorna i meter, C är kapacitansen i farad, ε är mediets dielektriska konstant. Alla värden som ingår i formeln anges i SI-systemet. Denna formel gäller för den enklaste platta kondensatorn: du kan helt enkelt placera två metallplattor bredvid dem, från vilka slutsatser dras. Luft kan fungera som ett dielektrikum.
Från denna formel kan man förstå att kondensatorns kapacitet är större, ju större är plattorna och desto mindre avståndet mellan dem. För kondensatorer med en annan geometri kan formeln vara annorlunda, till exempel för kapacitansen för en enda ledare eller elektrisk kabel. Men beroende av kapacitansen på plattorna och avståndet mellan dem är detsamma som för en platt kondensator: ju större området och desto mindre avståndet, desto större är kapacitansen.
Faktum är att plattorna inte alltid är plana. För många kondensatorer, till exempel, papper, är plattorna aluminiumfolie rullad tillsammans med ett dielektriskt papper i en tät boll i form av ett metallhölje.
För att öka den elektriska hållfastheten impregneras tunt kondensatorpapper med isolerande kompositioner, oftast transformatorolja. Denna design gör att du kan skapa kondensatorer med en kapacitet på upp till flera hundra mikrofarader. Kondensatorer med andra dielektrik är på liknande sätt anordnade.
Formeln innehåller inga begränsningar för plattorna S och avståndet mellan plattorna d.Om vi antar att plattorna kan spridas mycket långt, och samtidigt göra plattområdet mycket liten, kommer viss kapacitet, om än liten, fortfarande att kvarstå. Detta resonemang antyder att till och med bara två ledare i grannskapet har en elektrisk kapacitet.
Denna omständighet används ofta i högfrekvent teknik: i vissa fall tillverkas kondensatorer helt enkelt i form av tryckta kretsspår, eller till och med bara två ledningar tvinnade i polyetenisolering. Vanliga trådnudlar eller kabel har också kapacitet, och med ökande längd ökar den.
Förutom kapacitans C har alla kablar också motstånd R. Båda dessa fysiska egenskaper är fördelade längs kabelns längd, och när de överför pulsade signaler fungerar de som en integrerande RC-kedja, som visas i figur 2.

Figur 2
I figuren är allt enkelt: här är kretsen, här är insignalen, men här är det vid utgången. Impulsen är förvrängd bortom igenkännande, men detta görs avsiktligt för vilket kretsen är monterad. Under tiden pratar vi om effekten av kabelkapacitansen på pulssignalen. I stället för en impuls kommer en sådan "klocka" att visas i den andra änden av kabeln, och om impulsen är kort, kanske den inte når den andra änden av kabeln alls, kommer den att försvinna helt.
Historiskt faktum
Här är det ganska lämpligt att komma ihåg historien om hur den transatlantiska kabeln lades. Det första försöket 1857 misslyckades: telegrafpunkterna - streck (rektangulära pulser) förvrängdes så att inget kunde demonteras i den andra änden av 4000 km-linjen.
Ett andra försök gjordes 1865. Vid denna tid hade den engelska fysikern W. Thompson utvecklat teorin om dataöverföring över långa linjer. Mot bakgrund av denna teori visade sig kabeldirigeringen vara mer framgångsrik och vi kunde ta emot signaler.
För denna vetenskapliga prestation beviljade drottning Victoria forskaren riddaren och titeln Lord Kelvin. Det var namnet på den lilla staden vid Irlands kust, där kabelbeläggningen började. Men detta är bara ett ord, och nu återgår vi till den sista bokstaven i formeln, nämligen till dielektricitetskonstanten för mediet ε.
Lite om dielektrik
Detta e är i nämnaren för formeln, därför kommer dess ökning att innebära en ökning av kapaciteten. För de flesta dielektriker som används, såsom luft, lavsan, polyeten, fluoroplast, är denna konstant nästan densamma som för vakuum. Men samtidigt finns det många ämnen vars dielektriska konstant är mycket högre. Om luftkondensorn är fylld med aceton eller alkohol, ökar dess kapacitet varje 15 ... 20.
Men sådana ämnen, förutom hög e, har också en tillräckligt hög konduktivitet, därför kommer en sådan kondensator inte att hålla en laddningsbrunn, den kommer snabbt att urladdas genom sig själv. Detta skadliga fenomen kallas läckström. Därför utvecklas speciella material för dielektrik som med en hög specifik kapacitans för kondensatorer ger acceptabla läckströmmar. Detta förklarar mångfalden av typer och typer av kondensatorer, som var och en är utformade för specifika förhållanden.
Elektrolytisk kondensator
Den största specifika kapaciteten (kapacitet / volymförhållande) elektrolytiska kondensatorer. Kapaciteten för "elektrolyter" når upp till 100 000 mikrofarader, och driftspänningen är upp till 600V. Sådana kondensatorer fungerar bra endast vid låga frekvenser, oftast i filter för strömförsörjning. Elektrolytiska kondensatorer slås på i polaritet.
Elektroderna i sådana kondensatorer är en tunn film av metalloxid, så ofta kallas dessa kondensatorer oxid. Ett tunt luftskikt mellan sådana elektroder är inte en särskilt tillförlitlig isolator, därför införs ett elektrolytskikt mellan oxidplattorna. Oftast är dessa koncentrerade lösningar av syror eller alkalier.
Figur 3 visar en av dessa kondensatorer.

Bild 3. Elektrolytisk kondensator
För att utvärdera kondensatorns storlek fotograferades en enkel matchbox bredvid. Förutom en tillräckligt stor kapacitet i figuren kan du också se den procentuella toleransen: inte mindre än 70% av den nominella.
På de dagar då datorer var stora och kallade datorer fanns sådana kondensatorer i enheter (i modern HDD). Informationskapaciteten för sådana enheter kan nu bara ge ett leende: 5 megabyte information lagrades på två diskar med en diameter på 350 mm, och enheten själv vägde 54 kg.
Det huvudsakliga syftet med superkondensatorerna som visas i figuren var att magnetiska huvuden dras ur skivans arbetsområde under ett plötsligt strömavbrott. Sådana kondensatorer kunde lagra en laddning i flera år, som testades i praktiken.
Lite lägre med elektrolytiska kondensatorer kommer att erbjudas att göra några enkla experiment för att förstå vad en kondensator kan göra.
För att arbeta i växelströmskretsar produceras icke-polära elektrolytkondensatorer, det är bara svårt att få dem av någon anledning. För att på något sätt komma runt detta problem inkluderar vanliga polära "elektrolyter" motsekvens: plus-minus-minus-plus.
Om den polära elektrolytkondensatorn ingår i växelströmskretsen, kommer den först att värmas upp och sedan hörs en explosion. Inhemska gamla kondensatorer spridda i alla riktningar, medan importerade har en speciell enhet som undviker höga bilder. Detta är vanligtvis antingen ett tvärspår på kondensatorns botten eller ett hål med en gummipropp på samma plats.
De gillar inte elektrolytiska kondensatorer med ökad spänning, även om polariteten observeras. Därför ska du aldrig sätta "elektrolyter" i en krets där en spänning som är nära det maximala för en given kondensator förväntas.
Ibland ställer nybörjare i vissa, även ansedda forum, frågan: "Kondensatorn 470μF * 16V visas på diagrammet, och jag har 470μF * 50V, kan jag säga det?" Ja, det kan du naturligtvis, men det omvända utbytet är inte tillåtet.
Kondensator kan lagra energi
För att hantera detta uttalande hjälper ett enkelt diagram som visas i figur 4.
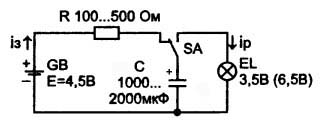
Bild 4. Krets med kondensator
Protagonisten i denna krets är en elektrolytisk kondensator C med tillräckligt stor kapacitet att laddnings-urladdningsprocesserna går långsamt och till och med mycket tydligt. Detta gör det möjligt att observera kretsens funktion visuellt med användning av ett konventionellt ljus från en ficklampa. Dessa lampor har länge gett plats för moderna lysdioder, men lampor för dem säljs fortfarande. Därför är det mycket enkelt att montera en krets och utföra enkla experiment.
Kanske någon kommer att säga: ”Varför? Allt är ju uppenbart, och även om du läser beskrivningen ... ” Det verkar inte finnas något att argumentera här, men något, till och med det enklaste, kvarstår i huvudet länge om dess förståelse kom genom händerna.
Så kretsen är monterad. Hur fungerar hon?
I stället för omkopplaren SA, som visas i diagrammet, laddas kondensatorn C från strömkällan GB genom motståndet R i kretsen: + GB __ R __ SA __ C __-GB. Laddningsströmmen i diagrammet visas med en pil med indexet iз. Processen att ladda en kondensator visas i figur 5.
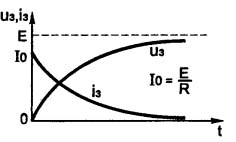
Bild 5. Kondensatorladdningsprocess
Figuren visar att spänningen på kondensatorn ökar längs en kurva, i matematik som kallas exponenten. Laddströmmen speglar direkt laddningsspänningen. När spänningen över kondensatorn stiger blir laddningsströmmen mindre och mindre. Och endast i det första ögonblicket motsvarar formeln som visas i figuren.
Efter en tid laddas kondensatorn från 0V till spänningen på strömkällan, i vår krets till 4,5V. Hela frågan är, hur är det dags att avgöra hur lång tid att vänta, när kommer kondensatorn att ladda?
Tau tidskonstant τ = R * C
I denna formel multipliceras helt enkelt motståndet och kapacitansen för ett seriekopplat motstånd och kondensator.Om, utan att försumma SI-systemet, ersätta motståndet i Ohms, kapacitansen i Farads, blir resultatet i sekunder. Det är den här gången som krävs för att kondensatorn laddar upp till 36,8% av spänningen i kraftkällan. Följaktligen krävs en tid på 5 * t för en avgift på nästan 100%.
Ofta, genom att försumma SI-systemet, ersätts resistansen i Ohms i formeln, och kapacitansen är i mikrofarader, då kommer tiden att visa sig i mikrosekunder. I vårt fall är det bekvämare att få resultatet i sekunder, för vilket du bara måste multiplicera mikrosekunderna med en miljon, eller, mer enkelt uttryckt, flytta kommateckens sex tecken till vänster.
För kretsen som visas i figur 4, med en kondensator på 2000 μF och ett motståndsmotstånd på 500 Ω, kommer tidskonstanten att vara τ = R * C = 500 * 2000 = 1 000 000 mikrosekunder eller exakt en sekund. Därför måste du vänta i cirka 5 sekunder tills kondensatorn är fulladdad.
Om omkopplaren SA vrids till rätt läge efter att den angivna tiden har gått, tappas kondensatorn C genom EL-glödlampan. Just nu kommer en kort blixt att ske, kondensatorn kommer att urladdas och ljuset slocknar. Kondensatorns urladdningsriktning visas med en pil med indexet ip. Urladdningstiden bestäms också av tidskonstanten τ. Urladdningsgrafen visas i figur 6.
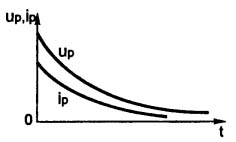
Figur 6. Graf för urladdning av kondensator
Kondensator passerar inte likström
För att verifiera detta uttalande hjälper ett ännu enklare schema som visas i figur 7.
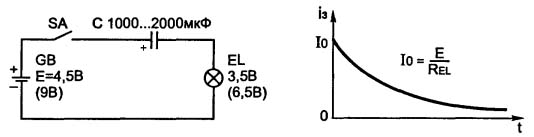
Bild 7. Krets med kondensator i DC-kretsen
Om du stänger omkopplaren SA följer en kort blixt av lampan, vilket indikerar att kondensatorn C laddas genom lampan. Laddningsgrafen visas också här: just nu brytaren stängs är strömmen maximal, eftersom kondensatorn laddar minskar den och efter ett tag stannar den helt.
Om kondensatorn är av god kvalitet, d.v.s. med en liten läckström (självutladdning) kommer den upprepade stängningen av strömställaren inte att leda till blixt. För att få ytterligare blixt måste kondensatorn urladdas.
Kondensator i kraftfilter
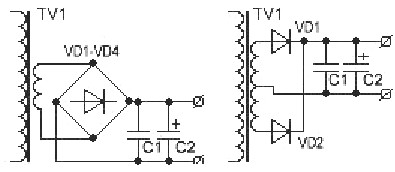
Kondensatorn placeras vanligtvis efter likriktaren. Oftast görs likriktare halvvågiga. De vanligaste likriktarkretsarna visas i figur 8.
Bild 8. Likriktarkretsar
Halvvåglikriktare används också ganska ofta, i regel i de fall då lastkraften är obetydlig. Den mest värdefulla kvaliteten på sådana likriktare är enkelhet: endast en diod och transformatorlindning.
För en halvvågslikriktare kan filterkondensatorns kapacitet beräknas med formeln
C = 1 000 000 * Po / 2 * U * f * dU, där C är kondensatorn μF, Po är lasteffekten W, U är spänningen vid likriktarens utgång V, f är frekvensen för växelspänningen Hz, dU är kretsamplituden V
Ett stort antal i räknaren på 1 000 000 konverterar kondensatorns kapacitans från system Farads till mikrofarader. De två i nämnaren representerar antalet halva perioder av likriktaren: för en halvvåg på sin plats kommer en enhet att dyka upp
C = 1 000 000 * Po / U * f * dU,
och för en trefas likriktare kommer formeln att ha formen C = 1 000 000 * Po / 3 * U * f * dU.
Supercapacitor - Ionistor
Nyligen har en ny klass av elektrolytiska kondensatorer, den så kallade ionistor. I sina egenskaper liknar det dock ett batteri med flera begränsningar.
Jonistorn laddar den nominella spänningen på kort tid, bokstavligen på några minuter, så det är tillrådligt att använda den som en reservkraftkälla. I själva verket är jonistorn en icke-polär enhet, det enda som bestämmer dess polaritet är laddning på fabriken. För att inte förväxla denna polaritet i framtiden indikeras den med + -tecknet.
En viktig roll spelas av driftsförhållandena för jonistorerna. Vid en temperatur på 70 ° C vid en spänning på 0,8 av den nominella garanterade hållbarheten på högst 500 timmar.Om enheten fungerar med en spänning på 0,6 från den nominella och temperaturen inte överstiger 40 grader, är korrekt drift möjlig i 40 000 timmar eller mer.
De vanligaste jonistortillämpningarna är reservkällor. Dessa är främst minneschips eller elektroniska klockor. I detta fall är ionistorns huvudparameter en låg läckström, dess självutladdning.
Ganska lovande är användningen av jonistorer i samband med solpaneler. Det påverkar också icke-kritik till laddningens tillstånd och ett nästan obegränsat antal laddnings-urladdningscykler. En annan värdefull egenskap är att jonistorn är underhållsfri.
Hittills har det visat sig berätta hur och var elektrolytkondensatorer fungerar, och främst i DC-kretsar. Funktionen av kondensatorer i växelströmskretsar kommer att beskrivas i en annan artikel - Kondensatorer för elinstallationer.
Boris Aladyshkin
P.S. Ett intressant användningsfall för kondensatorer: kondensatorsvetsning
Se även på elektrohomepro.com
: